by R. Grothmann
Compute the probability to get a choice with different objects, if m of out of n are chosen randomly. The formula is of course
![]()
We use the prod formula of Euler for this.
>function map f(m,n) := prod((n:-1:n-m+1)/n)
The following is the chance to get 5 different numbers, if 5 are chosen from 10 numbers.
>f(5,10)
0.3024
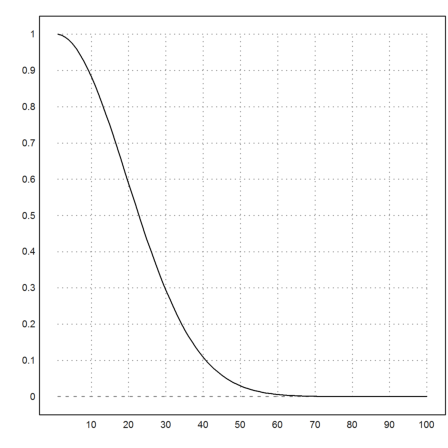
It is an almost safe bet, that there are at least two out of 60 persons with same birthday.
>f(60,365)
0.00587733913465
The bet on this event becomes favorable with more than 23 people.
>m=1:100; plot2d(m,f(m,365)):
Let us investigate Lotto in a small town like Eichstätt, Germany (assuming 10000 Lotto players). Chances are 1:36 against all Lotto sheets being different.
>n=bin(49,6)
13983816
>1/f(10000,n)
35.7323646644
For large n and m, it is better to use an approximation using Sterling's formula.
>function map fa(m,n) := sqrt(n/(n-m))*(n/(n-m))^(n-m)*exp(-m) >fa(60,365)
0.00587760311246
>f(60,365)
0.00587733913465
When does the probability pass 0.5 in our birthday problem?
>bisect("fa(x,365)-0.5",20,30)
22.7679316109
In Euler, the bisection method works for discrete functions.
>bisect("f(x,365)-0.5",20,30)
23
Indeed, the switch is between 22 and 23.
>f(21:30,365)
[0.556312, 0.524305, 0.492703, 0.461656, 0.4313, 0.401759, 0.373141, 0.345539, 0.319031, 0.293684]
We simulate the choice with a Monte Carlo simulation. The following function returns the percentage of j equal entries when choosing m out of n.
>function simulate (m,n,k=100000) ... res=zeros(1,m); loop 1 to k h=floor(random(1,m)*n); j=max(count(h[1:m],n)); res[j]=res[j]+1; end; j=max(nonzeros(res<>0)); return res[1:j]/k; endfunction
We select 200 people 100000 times. It is very likely to find three or more with same birthday.
>res=simulate(200,365); plot2d(res,bar=1):
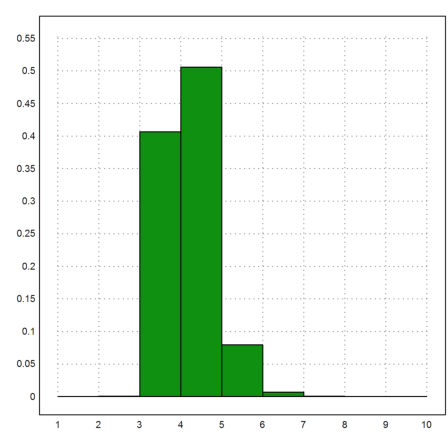
The simulated result is close to the theoretical result.
>res=simulate(40,365); res[1], f(40,365),
0.1099 0.108768190182
When selecting 5 out of 10, finding 2 equal numbers has the largest chance.
>res=simulate(5,10); plot2d(res,bar=1):
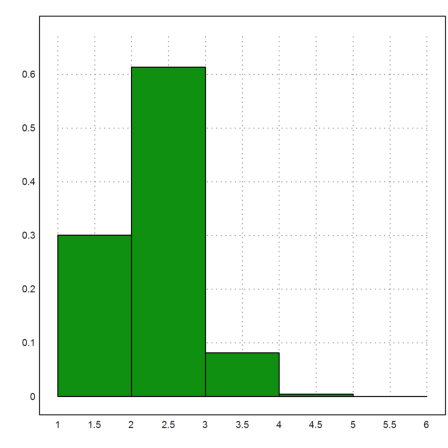
The simulation result is close to the theoretical result.
>res[1], f(5,10),
0.30068 0.3024
What is the average waiting time until two persons with same birthday are found? We observe that the chance to find the first same birthday at the i-th person is f(i-1,n)*(i-1)/n, since the first i-1 must be different from each other and the next one must be one of the first i-1.
>n=365; i=2:n; sum(fmap(i-1,n)*(i-1)/n*i)
24.6165858946
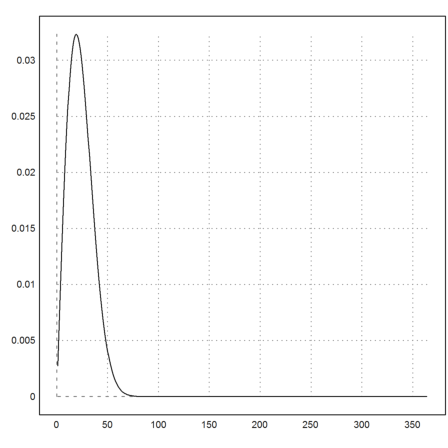
Here is a distribution of the waiting time.
>plot2d(fmap(i-1,n)*(i-1)/n):